T-SIM V4.5 Reference
K-BKZ model
The K-BKZ non-linear and time-dependent
viscoelastic material was proposed by Kaye [1] and Bernstein et al.
[2]. The time-integral constitutive equation of the K-BKZ model is
![]() (1),
(1),
where ![]() is
the stress tensor, m (t-t’) is
a time-memory function, h(I1,I2) is a damping
function of the two strain invariants I1,I2 and
is
the stress tensor, m (t-t’) is
a time-memory function, h(I1,I2) is a damping
function of the two strain invariants I1,I2 and
![]() is the
Finger strain tensor. Temperature effects are included via an Arrhenius
temperature dependency of material parameters. Furthermore, we have:
is the
Finger strain tensor. Temperature effects are included via an Arrhenius
temperature dependency of material parameters. Furthermore, we have:
Time-memory function:
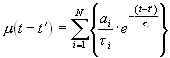 (2)
(2)
where ai are the relaxation modulus, ti are the relaxation times and N is the number of the pairs modul / time.
The damping function h(I1,I2) can be one of the following:
![]() (3)
(3)
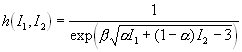 (4)
(4)
![]() (5)
(5)
where a, b are adjustable parameters, I1, I2 are the first and the second invariants of the Finger strain tensor given by:
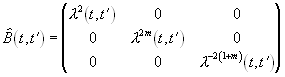 (6)
(6)
![]() (7)
(7)
where l is the extension ratio.
Table 1 shows values of the m parameter for various types of deformation:
Table 1: Values of m for some types of deformation:
|
Type of deformation |
m |
|
Uniaxial elongation |
-1/2 |
|
Planar extension (pure shear) |
0 |
|
Ellipsoidal extension |
1/2 |
|
Equibiaxial extension |
1 |
The damping functions (eq. 3, 4) were suggested by Wagner [3,4]. The damping function (eq. 5) was proposed by Papanastasiou et al. [5].
Invariants of Finger strain tensor:
![]() (8)
(8)
![]() (9)
(9)
![]()
Finger strain tensor for uniaxial elongation:
![]()
![]()
![]() (10)
(10)
Finger strain tensor biaxial extension ( l (t) is the same for both directions):
![]()
![]()
![]() (11)
(11)
Equations for stresses in principal directions:
![]() (12)
(12)
![]() (13)
(13)
[1] Kaye, A.: ”Non-Newtonian Flow in Incompressible Fluids”, College of Aeronautics, Cranfield, CoA Note No. 134 (1962)
[2] Bernstein, B., Kearsley, E.A., Zapas, L.J.: Trans. Soc. Rheol. 7, p.391/410 (1963)
[3] Wagner, M.H.: J. Rheol. 34(6), p.943/958 (1990)
[4] Wagner, M.H.: Rheol. Acta 15, p.136/142, (1976)
[5] Papanastasiou, A.C., Scriven, L.E., Macosko, C.W.: J. Rheol. 27(4), p.387/410 (1983)